혹시 1년이 몇일인지 아시나요?

2010년 새해가 시작되었다. 해가 바뀌면서 마음가짐도 새롭게 하고 주변도 정리하면서 한 해를 열심히 살아보자고 스스로 다짐도 하여 본다. 새해가 되면서 바뀌는 것이 마음가짐 말고도 많지만, 이 가운데 당장 눈에 띄는 것은 아마도 달력이 아닐까 싶다. 우리가 현재 사용하는 달력의 구조를 살펴보자.

 

 

 

1년은 과연 며칠인가? 고대로부터 계절의 변화를 알려주는 달력은 대단히 중요한 도구였다. 특히 자연에 전적으로 의존해야 했던 농사에 달력은 없어서는 안 될 도구였다. 달력의 체계를 뜻하는 역법은 역사적으로, 또 과학적으로 여러 가지 방법이 가능한데, 가장 먼저 필요한 것은 1년의 길이이다. 이 길이를 재는 방법은 천문현상을 이용하는 것으로, 별자리를 관측하는 것이 기본이다. 고대 문명은 오랜 관찰을 통해 1년이 대략 360일 정도의 길이임을 알아내었다. 원을 한 바퀴 돌면 360도인 것도 바로 여기에서 유래하였다. 그러나 세월이 좀 더 흐르면서, 1년의 길이는 실제로는 360일보다 조금 더 길다는 사실을 알게 되어, 365일을 1년으로 하는 역법이 정착되었다. 그러나 다시 세월이 흐르면서, 365일로는 작지만 오차가 발생한다는 것이 알려져, 새로운 역법이 필요해졌다. 이때 등장하는 인물이 고대 로마의 정치가 율리우스 카이사르(Julius Caesar, BC100~BC44)이다.     율리우스력 - 기원전 46년은 445일!

로마 문명이 흔히 그랬던 것처럼, 로마의 새 역법은 로마인이 만든 것이 아니다. 고대의 달력에 문제가 있다는 것은 알았지만 정밀한 천문관측 결과가 부족하였던 로마는 이집트의 천문 지식을 통해 정밀한 1년의 길이를 알게 되었고, 이를 이용하여 새로운 역법을 만들었다. 과학적이라기보다는 실용적이었던 로마다운 해결책이라 하겠다. 카이사르는 이집트를 침략하여, 찬란했던 고대 이집트의 지식을 접하게 되었다. 그 가운데 이집트 인이 관측한 1년의 길이는 365일보다 조금 긴, 약 365.25일이었다. 즉, 4년 동안의 날수는 4×365=1,460일이 아니라, 하루가 더 긴 1,461일이라는 것이다. 당연한 말이지만, 매년 1/4일을 덧붙일 수는 없으므로, 카이사르는 4년마다 1년의 길이를 366일로 하는 역법을 도입하였다. 바로 윤일(閏日)의 개념이다. 윤일이 있는 해를 윤년, 윤일이 없는 해를 평년이라 한다. 카이사르가 개정한 이 역법은 카이사르의 이름을 따 “율리우스력”이라 한다. 이 역법은 대단히 정밀해서, 이후로 천 년이 넘게 사용되었다. 한 가지 재미있는 사실을 덧붙이자면, 카이사르가 역법을 바꾸기 전에 사용되던 로마의 달력은 음력을 기반으로 하여 달력과 계절의 차이가 너무 벌어져 있었다. 이런 이유로 카이사르는 90일에 달하는 윤달을 추가하여 기존의 달력과 계절을 맞추었다. 이 바람에 기원전 46년은 무려 445일이나 되는 역사상 가장 긴(?) 해가 되었다.

 

 

그레고리력 - 1582년의 달력에는 열흘이 없다! 큰 문제 없이 사용되던 율리우스력은 천 년이 넘어가면서 문제점을 드러내기 시작하였다. 가톨릭이 지배하던 16세기 유럽. 기독교의 가장 중요한 기념일인 부활절의 날짜를 정하는 데에 심각한 문제가 발생하였다. 원래 부활절은 춘분 다음 보름이 지난 첫 일요일로 정해지는데, 처음에 부활절을 제정하던 서기 325년에는 3월 21일이던 춘분이 율리우스력의 오차 때문에 조금씩 앞당겨져 1300년 정도가 흐르자 10일까지 차이가 생긴 것이다. 즉, 1년의 길이가 율리우스력의 365.25일보다는 약간 짧은 365.2422일 정도여서, (365.25-365.2422) ×1300=10.14일의 차이가 생긴다. 이 문제를 해결하기 위해, 당시 교황이던 그레고리우스 13세는 우선 1582년 10월 4일 다음 날을 10월 15로 정하여 열흘의 날짜를 줄여, 춘분이 3월 21일이 되도록 맞추었다. 그다음으로 윤일을 율리우스력보다 줄이기 위하여, 다음과 같은 규칙을 정하였다.                   1. 그 해의 연도가 4의 배수가 아니면, 평년으로 2월은 28일까지만 있다.                 2. 만약 연도가 4의 배수이면서 100의 배수가 아니면, 윤일(2월 29일)을 도입한다.                 3. 만약 연도가 100의 배수이면서 400의 배수가 아닐 때, 이 해는 평년으로 생각한다.                 4. 만약 연도가 400의 배수이면, 윤일(2월 29일)을 도입한다.   이와 같은 규칙을 따르면, 400년 동안 총 97일의 윤일이 더해지므로, 1년의 길이가 365+97/400=365.2425일이 되어 율리우스력보다 더욱 정밀해진다.   러시아 정교회의 성탄절은 1월 7일 과학적으로 생각하면 그레고리력을 사용하는 것이 당연하겠지만, 가톨릭의 수장인 교황이 제정하였다는 이유로 이 역법을 사용하지 않은 지역이 적지 않았다. 심지어 로마 가톨릭과 다른 동방 정교회(orthodox)의 그리스와 러시아는 20세기 초까지도 율리우스력을 사용하여, 날짜 때문에 웃지 못할 사건·사고가 많았다. 러시아 정교회의 성탄절이 12월 25일 대신 1월 7일인 것도 러시아가 그레고리력을 늦게 채택한 때문에 벌어진 일이었다. 러시아 정교회는 여전히 율리우스력으로 날짜를 헤아리기 때문에, 율리우스력 12월 25일은 그레고리력으로는 다시 하루가 더 벌어져 11일 차이가 나는 1월 7일이 되어 있기 때문이다. 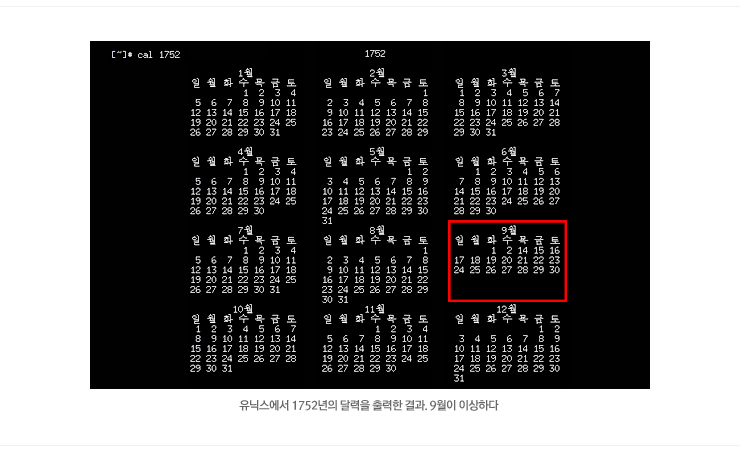다음 그림은 유닉스(UNIX) 시스템에서 cal 명령어를 이용하여 1752년의 달력을 출력한 것이다.  9월 달력에 3일부터 13일까지 11일이 빠져 있음을 볼 수 있다. 이것은 영국이 그레고리력을 1752년에 채택한 사실을 반영한 것이다.

 

 

 

그레고리력으로 충분할까? 앞서 보았듯, 그레고리력은 1년을 365.2425일로 정하고 있는데, 이 값은 365.2422일이라는 관측 값과는 작으나마 0.0003만큼 차이가 난다. 따라서 10,000년이 지나면 3일 정도의 차이가 생기게 된다. 이런 이유로 영국의 수학자 허셸(John Herschel, 천왕성을 발견한 천문학자 허셸의 아들)은 연도가 4,000의 배수일 때는 평년으로 정할 것을 제안하였다. 원래의 그레고리력에서는 4,000은 400의 배수이므로 윤년이 되어야 하지만, 허셸의 제안을 따르면 4,000년 동안 총 97×10-1=969일의 윤일이 있게 된다. 그 결과, 1년의 평균 길이는 365 + 969/4000 = 365.24225일이 되어 기존의 그레고리력보다 더욱 정밀해진다. 그러나 지구가 태양 주위를 도는 속도가 항상 똑같은 것은 아니므로, 10,000년 후의 오차가 정말로 정확히 3일이 될지는 알 수 없는 일이다. 따라서 서기 4,000년을 윤년으로 해야 하는지 그럴 필요가 없는지는 서기 3,000년이 지난 다음에 결정해도 충분하다. 생각해 보면, 100년도 채 못사는 인간이 1,000년 후, 2,000년 후의 일에 신경 쓴다는 게 놀랍기도 하다. 이것은 자연이 따르는 수학적 법칙을 인간이 인식할 수 있었기에 가능한 일이다.

 

<출처 : 네이버 캐스트 (http://navercast.naver.com/science/math/1793) >